REPASO
1) Construir una tabla que resuma las operaciones necesarias para convertir números entre los sistemas binarios, octal , decimal y hexadecimal.

2) Completar la siguiente tabla indicando debajo de la misma las operaciones realizadas.
Binario
|
Octal
|
Decimal
|
Hexadecimal
| |
Binario
|
11101,01
|
35,2
|
29,25
|
1D,4
|
Octal
|
110011,111010
|
63,72
|
51,906
|
33,E8
|
Decimal
|
11111110,01
|
376,2
|
254,25
|
FE,4
|
Hexadecimal
|
001100101011001010,111111101010
|
145312,7752
|
51914,9935
|
CACA,FEA
|
3) Para las compuertas and, or y xor de 2, 3 y 4 entradas:
- función
- símbolo
- tabla de verdad
COMPUERTA AND
A
|
B
|
F
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
función: F = A · B · C
A
|
B
|
C
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
funcion: F = A · B · C · D
A
|
B
|
C
|
D
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
COMPUERTA OR
función: F = A + B
A
|
B
|
F
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
función: F = A + B + C
A
|
B
|
C
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
función: F = A + B + C + D
A
|
B
|
C
|
D
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
COMPUERTA XOR
A
|
B
|
F
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
A
|
B
|
C
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
A
|
B
|
C
|
D
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
COMPUERTA NAND
tabla de verdad:
A
|
B
|
C
|
F
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
 |
| SÍMBOLO |
COMPUERTA NOR
tabla de verdad:
A
|
B
|
C
|
F
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
 |
| SÍMBOLO |
COMPUERTA XNOR
4) Para las siguientes funciones dar circuito y tabla de verdad.
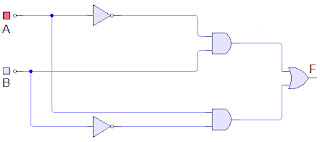
5) Para los siguientes circuitos dar funcion y tabla de verdad.
A_
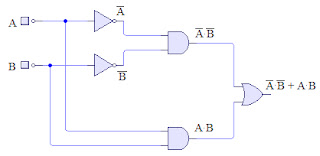

6) Verificar las leyes de de Morgan mediante tablas de verdad. Dibujar los circuitos.
8)
Para un puente angosto circulan tres lineas ferroviarias. Por razones
de seguridad se quiere impedir que circulen dos formaciones adyacentes.
Para eso se ha colocado una señal de detención en el carril central.
Desarrollar un circuito lógico que encienda la señal cuando
la situación lo requiera.
9) Para las siguientes tablas de verdad dar la función por miniterminos y maxterminos. Dibujar los circuitos.
10) Construir un circuito digital capaz de comparar dos numeros de 1 bit. Indicando con un 1 en las saludas correspondientes las siguientes condiciones: A<B, A=B, A>B

11) Construir un circuito que se comporte como una compuerta xnor a partir de la funcion obtenida por miniterminos y maxterminos de 3 entradas.
12) Construir un circuito que se comporte como una compuerta xor de 2 entradas.
a) utilizando solamente compuertas nand.
b) utilizando solamente compuertas nor.
13) Construir el circuito del comparador (ejercicio Nº10)
a) utilizando solamente compuertas nand.
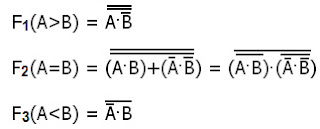

b) utilizando solamente compuertas nor.


14) Construir el circuito del ejercicio Nº8 (punete angosto) utilizando solamente compuertas nand.

A
|
B
|
C
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
9) Para las siguientes tablas de verdad dar la función por miniterminos y maxterminos. Dibujar los circuitos.
A
|
B
|
F
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
A
|
B
|
C
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
A
|
B
|
C
|
D
|
F
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
10) Construir un circuito digital capaz de comparar dos numeros de 1 bit. Indicando con un 1 en las saludas correspondientes las siguientes condiciones: A<B, A=B, A>B
A
|
B
|
A<B
|
A=B
|
A>B
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|

11) Construir un circuito que se comporte como una compuerta xnor a partir de la funcion obtenida por miniterminos y maxterminos de 3 entradas.
A
|
B
|
C
|
XNOR
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
12) Construir un circuito que se comporte como una compuerta xor de 2 entradas.
a) utilizando solamente compuertas nand.
Obtener la F
por militerminos.
Negar 2 veces la función.
b) utilizando solamente compuertas nor.
Obtener la F
por maxterminos.
Negar 2 veces la función.
Aplicar Ley de De Morgan.
13) Construir el circuito del comparador (ejercicio Nº10)
a) utilizando solamente compuertas nand.
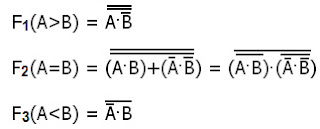

b) utilizando solamente compuertas nor.


14) Construir el circuito del ejercicio Nº8 (punete angosto) utilizando solamente compuertas nand.
A
|
B
|
C
|
F
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|